Background-Handcrafted Methods

Resampling Detection을 위한 hand-crafted methods 조사

  1. Exposing digital forgeries by detecting traces of resampling
    1. Abstract
    2. 1. Resampling Signals
    3. 2. Detecting Resampling
    4. 3. Resampling Images
  2. Blind Authentication Using Periodic Properties of Interpolation
    1. Abstract
    2. 1. Region of Interest(ROI) Selection
    3. 2. Signal Derivative Computation
    4. 3. Radon Transformation
    5. 4. Search for Periodicity

Exposing digital forgeries by detecting traces of resampling

Popescu, Alin C., and Hany Farid. “Exposing digital forgeries by detecting traces of resampling.” IEEE Transactions on signal processing 53.2 (2005): 758-767.

Abstract

  • forgery는 이미지의 underlying statistics을 바꾸는 특징을 가짐.
  • resampling (e.g., scaling or rotating)에 specific statistical correlations이 적용됨 설명
  • 이러한 상관 관계가 이미지의 모든 부분에서 어떻게 자동으로 감지 될 수 있는지 설명

1. Resampling Signals

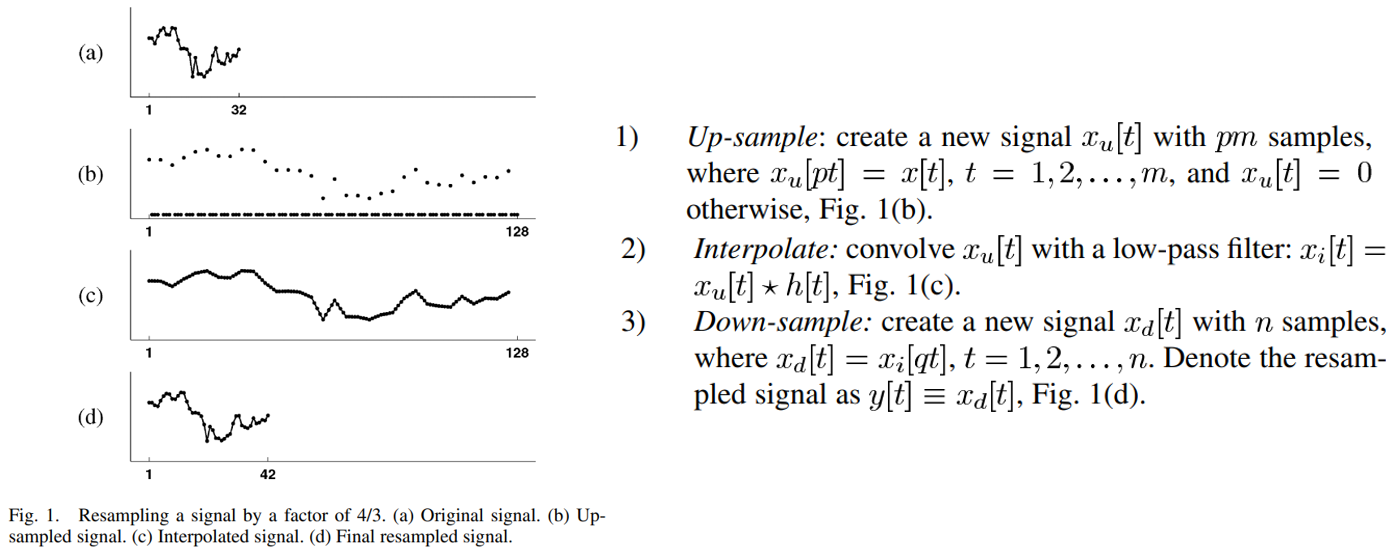
  • 샘플이있는 1-D 이산 샘플링 된 신호
  • fig1: 1차원 signal을 4/3만큼 resampling 하는 예시
    • (a): original signal
    • (b): 먼저 기존 신호에 4배 up-sampling 한다.
    • (c): 사이사이 빈 값을 채우기 위해 interpolation을 적용한다.
    • (d): 이렇게 만들어진 신호를 3배 down-sampling한다.
  • 위 과정은 single linear equation으로 정의될 수 있음.
\[\begin{aligned} \vec{y} &= A_{p/q}\vec{x}\\ \end{aligned}\]

이 신호의 샘플 수는 세 단계에서 n샘플에 대한 계수(p, q)만큼 증가 또는 감소

  • 위와 같은 조건을 통해 resampling된 신호 감지 가능 & “correlations are periodic”

2. Detecting Resampling

  • 이웃 픽셀과의 상관성을 갖는 주기적 samples를 찾음으로써 detect가능

3. Resampling Images

  • 이미지의 up-sampling or down-sampling은 선형 & 위와 동일한 과정 포함
  • correlation; 1D 신호와 마찬가지로 주기적
ScalingRotation

Blind Authentication Using Periodic Properties of Interpolation

Mahdian, Babak, and Stanislav Saic. “Blind authentication using periodic properties of interpolation.” IEEE Transactions on Information Forensics and Security 3.3 (2008): 529-538.

Abstract

  • 신호와 그것의 미분이 가져온 주기적 특성 사용 → resampling and interpolation의 흔적 감지 방법 소개
  • affine transformation을 구성하는 individual transformation에 주목함.
  • 4가지 방법으로 구성
    1. ROI selection
    2. signal derivative computation
    3. radon transformation
    4. search for periodicity

1. Region of Interest(ROI) Selection

  • typical image f(x,y); 여러개의 일관된 영역으로 구성
  • 해당 영역의 resampling 여부 조사
    • RxR 픽셀 블록(b(x,y))으로 해당 영역 선택 (R; 128)
    • 좌측상단에서 우측하단까지 수평으로 이동
  • image subset에 적용

2. Signal Derivative Computation

  • resampling된 이미지의 covariance(공분산) 구조; 주기적 특성을 강조하기위해 b(x,y)영역의 n차 도함수 계산
  • b(x, y)의 행의 인접 픽셀간의 차이를 계산하는 도함수 연산자 사용하여 수행(실제 실험에서는 n = 2로 설정)
\[\begin{aligned} D^n{b(x,y)} \end{aligned}\]

n차 도함수 계산

3. Radon Transformation

  • affine transformation의 흔적을 찾기 위해 radon 변환 사용 => 차원의 변화(2차원 signal -> 1차원 signal)
  • 각도 델타에 의해 결정된 지정의 방향을 따라 크기의 투영 계산
  • pixel을 4개의 sub-pixel로 나눠서 개별적으로 투영
  • 0-179도 사이의 각도에서 1도씩 증가하며 계산됨.

4. Search for Periodicity

  • resample → autocovariance sequences은 강한 주기성을 나타냄
  • 목표는 affine transformation의 적용 여부를 확인하는 것 → 공분산 section에서 존재하는 가장 강력한 주기적 패턴만 감지 가능
\[\begin{aligned} R_{\rho_\theta}(k) = \sum_i(\rho_\theta(i+k)-\bar{\rho_\theta})(\rho_\theta(i)-\bar{\rho_\theta}) \end{aligned}\]
Original ImageResampling Image

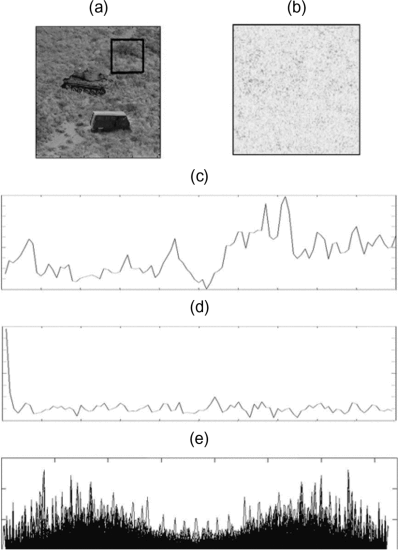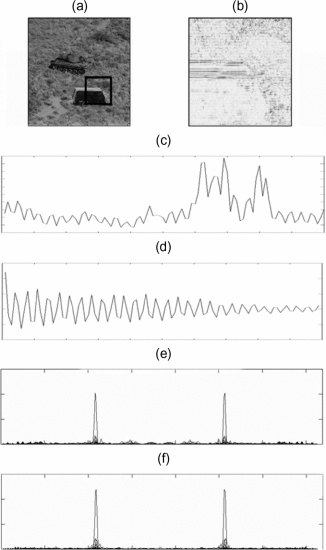(a) The investigated region b(x,y) (denoted by a black box, 128 × 128 pixels)(b) The magnitudes of the rows-based signal derivative (c) The radon transformation output (d) The autocovariance (e) The row-based output of the proposed method


위 논문을 기반으로 resampling detector를 구현하였습니다.

https://github.com/Sang-Yeong/image-forgery-detection


Continue with Related Work

해당 포스트는 아래를 참고하여 작성되었습니다.